快速计算约数的个数——从基础到高级
题目来源:【欧拉计划第 12 题】 高度可除的三角数 Highly divisible triangular number
这道题我们在枚举完三角数后,最重要的是去判断何时某个三角数约数的个数大于 500
下面我们来看下,针对计算约数的个数问题,用不同的算法解决,逐步求得最优解
题目来源:【欧拉计划第 12 题】 高度可除的三角数 Highly divisible triangular number
这道题我们在枚举完三角数后,最重要的是去判断何时某个三角数约数的个数大于 500
下面我们来看下,针对计算约数的个数问题,用不同的算法解决,逐步求得最优解
做世界级的 OS,让万物互联,信息畅通无阻。成为未来 AIoT 领域最为主流的操作系统平台。
RT-Thread 是一个集
实时操作系统(RTOS)内核、中间件组件和开发者社区于一体的技术平台,由熊谱翔先生带领并集合开源社区力量开发而成,RT-Thread 也是一个组件完整丰富、高度可伸缩、简易开发、超低功耗、高安全性的物联网操作系统。
RT-Thread 具备一个 IoT OS 平台所需的所有关键组件,例如GUI、网络协议栈、安全传输、低功耗组件等等。经过11年的累积发展,RT-Thread 已经拥有一个
国内最大的嵌入式开源社区,同时被广泛应用于能源、车载、医疗、消费电子等多个行业,累积装机量超过 14亿 台,成为国人自主开发、国内最成熟稳定和装机量最大的开源 RTOS。
RT-Thread 拥有
良好的软件生态,支持市面上所有主流的编译工具如 GCC、Keil、IAR 等,工具链完善、友好,支持各类标准接口,如 POSIX、CMSIS、C++应用环境、Javascript 执行环境等,方便开发者移植各类应用程序。商用支持所有主流MCU架构,如 ARM Cortex-M/R/A, MIPS, X86, Xtensa, C-Sky, RISC-V,几乎支持市场上所有主流的 MCU 和 Wi-Fi 芯片。
由飞利浦公司开发,支持设备间的短距离通信。i2c通信需要的引脚少,硬件实现简单、可扩展性强,被广泛应用在系统内多个集成电路(IC)间的通信。
i2c通信总线可连接多个i2c通信设备,支持多个通信主机和多个通信从机。i2c通信只需要两条双向总线——SDA(串行数据线)和SCL(串行时钟线)。SDA:用于传输数据SCL:用于同步数据收发
每个连接到总线的设备都有一个独立地址,共7bit,主机正是利用该地址对设备进行访问
i2c支持多主控,任何时间点都只能有一个主控。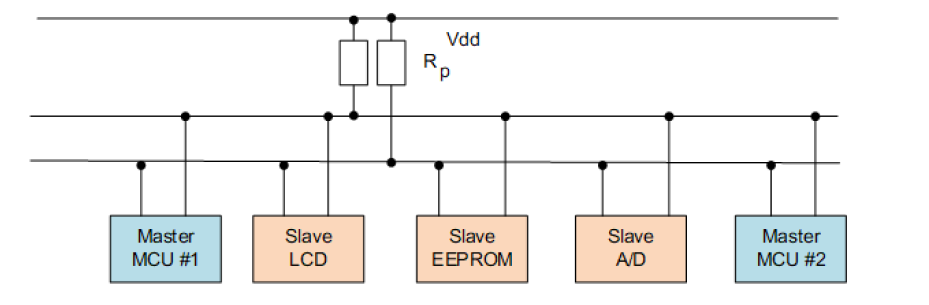
i2c器件的SDA引脚和SCL引脚是开漏电路形式,因此,SDA和SCL总线都需要连接上拉电阻,当总线空闲时,两条总线均为高电平。
各器件的SDA和SCL信号线在总线上都是线与关系。(即连接到总线上的任意器件输出低电平都会将总线信号拉低)
在日常生活中,我们通常会将一个大的问题拆分细化,拆开成若干个小问题,通过逐个解决小问题,大问题也就解决了。
同样的在RT-Thread多线程操作系统中,开发人员基于这种分而治之的思想,将一个复杂的应用问题抽象成若干个小的、可调度的、可序列化的程序单元。当合理地划分任务并正确地执行时,这种设计能够让系统满足实时系统的性能及时间的要求。
下面看一个例子:我们的任务是读取传感器上的数据,并将相关数据显示出来。通过拆分结构,我们可以发现主要有两个任务:
1.读取数据
2.显示数据
简单来说,就是一个子任务不间断地读取传感器数据,并将数据写到共享内存中,另外一个子任务周期性的从共享内存中读取数据,并将传感器数据输出到显示屏上。
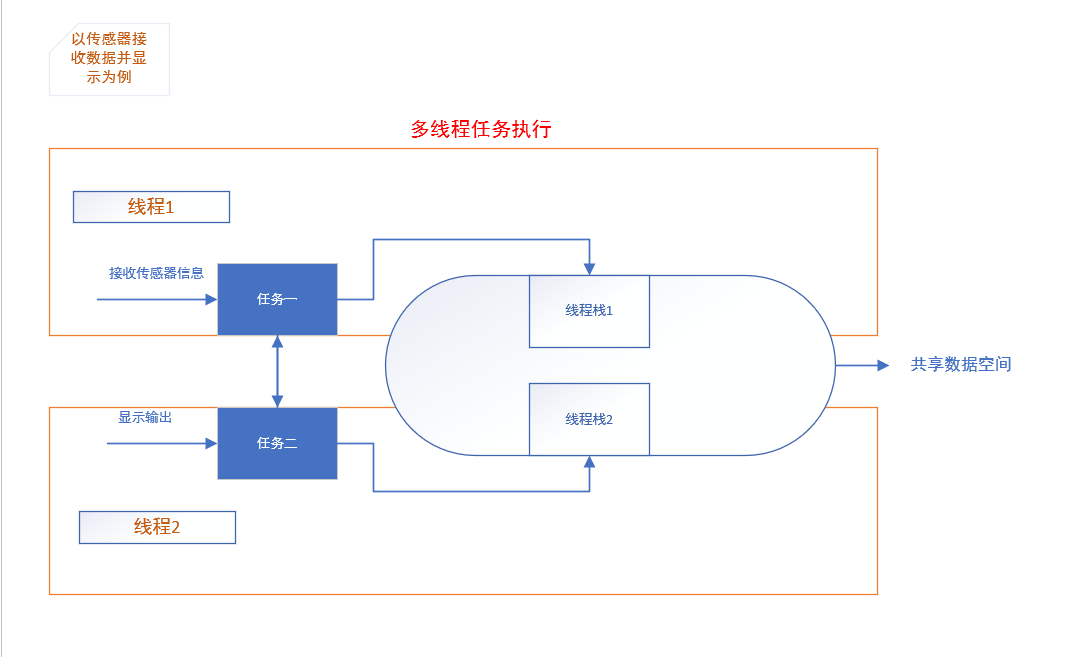
在RT-Thread 中,与上述子任务对应的程序实体就是线程,线程是实现任务的载体。
它是RT-Thread中最基本的调度单位,它描述了一个任务执行的运行环境,也描述了这个任务所处的优先等级,重要的任务可设置相对较高的优先级,非重要的任务可以设置较低的优先级,不同的任务还可以设置相同的优先级,轮流运行。上下文:当线程运行时,它会认为自己是以独占CPU 的方式在运行,线程执行时的运行环境称为上下文,具体来说就是各个变量和数据,包括所有的寄存器变量、堆栈、内存信息等。
The sequence of triangle numbers is generated by adding the natural numbers. So the 7th triangle number would be $1 + 2 + 3 + 4 + 5 + 6 + 7 = 28$. The first ten terms would be:
$$
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …
$$
Let us list the factors of the first seven triangle numbers:

We can see that $28$ is the first triangle number to have over five divisors.
What is the value of the first triangle number to have over five hundred divisors?